| Issue |
Ann. Phys. Fr.
Volume 28, Number 6, 2003
|
|
|---|---|---|
| Page(s) | 1 - 101 | |
| DOI | https://doi.org/10.1051/anphys:2004001 | |
| Published online | 15 November 2003 | |
Noble internal transport barriers and radial subdiffusion of toroidal magnetic lines
Barrières internes de transport " nobles " et sous-diffusion radiale des lignes magnétiques toroïdales
1
Association Euratom-C.E.A. sur la Fusion, CEA/DSM/DRFC,
C.E.A.-Cadarache, 13108 Saint-Paul-lez-Durance, France.
2
Association Euratom-M.E.C., Dept of Physics, University of
Craiova, Str. A.I. Cuza No 13, Craiova-1100, Romania.
3
Association Euratom-M.E.C., National Institute of Laser,
Plasma and Radiation Physics, P.O. Box MG-36, Magurele, Bucharest, Romania.
4
Association Euratom-État Belge sur la Fusion, Université
Libre de Bruxelles, CP 231, Campus Plaine, Boulevard du Triomphe, 1050 Bruxelles, Belgium.
Internal transport barriers (ITB's) observed in tokamaks are described by a
purely magnetic approach. Magnetic line motion in toroidal geometry with
broken magnetic surfaces is studied from a previously derived Hamiltonian
map in situation of incomplete chaos. This appears to reproduce in a
realistic way the main features of a tokamak, for a given safety factor
profile and in terms of a single parameter L representing the amplitude of
the magnetic perturbation. New results are given concerning the Shafranov
shift as function of L. The phase space ( ) of the
"tokamap" describes the poloidal section of the line trajectories, where
) of the
"tokamap" describes the poloidal section of the line trajectories, where 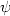 is the toroidal flux labelling the surfaces. For small values of L,
closed magnetic surfaces exist (KAM tori) and island chains begin to appear
on rational surfaces for higher values of L, with chaotic zones around
hyperbolic points, as expected. Island remnants persist in the chaotic
domain for all relevant values of L at the main rational q-values.
Single trajectories of magnetic line motion indicate the persistence of a
central protected plasma core, surrounded by a chaotic shell enclosed in a
double-sided transport barrier: the latter is identified as being composed
of two Cantori located on two successive “most-noble” numbers values of
the perturbed safety factor, and forming an internal transport barrier
(ITB). Magnetic lines which succeed to escape across this barrier begin to
wander in a wide chaotic sea extending up to a very robust barrier (as long
as
is the toroidal flux labelling the surfaces. For small values of L,
closed magnetic surfaces exist (KAM tori) and island chains begin to appear
on rational surfaces for higher values of L, with chaotic zones around
hyperbolic points, as expected. Island remnants persist in the chaotic
domain for all relevant values of L at the main rational q-values.
Single trajectories of magnetic line motion indicate the persistence of a
central protected plasma core, surrounded by a chaotic shell enclosed in a
double-sided transport barrier: the latter is identified as being composed
of two Cantori located on two successive “most-noble” numbers values of
the perturbed safety factor, and forming an internal transport barrier
(ITB). Magnetic lines which succeed to escape across this barrier begin to
wander in a wide chaotic sea extending up to a very robust barrier (as long
as  which is identified mathematically as a robust KAM surface
at the plasma edge. In this case the motion is shown to be intermittent,
with long stages of pseudo-trapping in the chaotic shell, or of sticking
around island remnants, as expected for a continuous time random walk.
For values of
which is identified mathematically as a robust KAM surface
at the plasma edge. In this case the motion is shown to be intermittent,
with long stages of pseudo-trapping in the chaotic shell, or of sticking
around island remnants, as expected for a continuous time random walk.
For values of  , above the escape threshold, most magnetic lines
succeed to escape out of the external barrier which has become a permeable
Cantorus. Statistical analysis of a large number of trajectories,
representing the evolution of a bunch of magnetic lines, indicate that the
flux variable
, above the escape threshold, most magnetic lines
succeed to escape out of the external barrier which has become a permeable
Cantorus. Statistical analysis of a large number of trajectories,
representing the evolution of a bunch of magnetic lines, indicate that the
flux variable  asymptotically grows in a diffusive manner as
asymptotically grows in a diffusive manner as  with a L2 scaling as expected, but that the average radial
position
with a L2 scaling as expected, but that the average radial
position  asymptotically grows as
asymptotically grows as  while the mean
square displacement around this average radius asymptotically grows in a
subdiffusive manner as
while the mean
square displacement around this average radius asymptotically grows in a
subdiffusive manner as  . This result shows the slower
dispersion in the present incomplete chaotic regime, which is different from
the usual quasilinear diffusion in completely chaotic situations. For
physical times
. This result shows the slower
dispersion in the present incomplete chaotic regime, which is different from
the usual quasilinear diffusion in completely chaotic situations. For
physical times 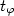 of the order of the escape time defined by
of the order of the escape time defined by  , the motion appears to be superdiffusive,
however, but less dangerous than the generally admitted quasi-linear
diffusion. The orders of magnitude of the relevant times in Tore Supra are
finally discussed.
, the motion appears to be superdiffusive,
however, but less dangerous than the generally admitted quasi-linear
diffusion. The orders of magnitude of the relevant times in Tore Supra are
finally discussed.
Résumé
Les barrières internes de transport observées dans les tokamaks
sont décrites ici dans une
approche purement magnétique. Le mouvement des lignes magnétiques en géométrie
toroïdale avec brisure des surfaces magnétiques est étudié à partir d'une application
hamiltonienne "tokamap" développée précédemment en situation de chaos incomplet, et
dans laquelle le "temps" est représenté par la coordonnée toroïdale. Cette application
reproduit de façon réaliste les principales caractéristiques d'un tokamak, pour un profil donné
du facteur de sécurité q, et en terme d'un seul paramètre L représentant l'amplitude de la
perturbation magnétique. On obtient des résultats nouveaux concernant le déplacement de
Shafranov en fonction de L. L'espace des phases  du "tokamap" décrit la section
poloïdale des trajectoires des lignes, où
du "tokamap" décrit la section
poloïdale des trajectoires des lignes, où  est le flux toroïdal caractérisant les surfaces
magnétiques (proportionnel au carré du rayon r de cette surface). Pour de faibles valeurs de L,
des surfaces magnétiques fermées existent (tores de KAM) et des chaînes d'îlots commencent
à apparaître sur les surfaces rationnelles pour des valeurs de L supérieures, avec, comme
attendu, des zones chaotiques autour des points hyperboliques. Des résidus d'îlots
magnétiques persistent dans le domaine chaotique pour toutes les valeurs de L, sur les
surfaces caractérisées par les principales valeurs rationnelles de q.
Des trajectoires individuelles de ligne magnétique indiquent la persistance d'un cœur protégé
au sein du plasma, entouré d'une couche chaotique, incluse dans une double barrière de
transport : celle-ci est composée de deux Cantori situés sur deux valeurs successives du facteur
de sécurité perturbé que l'on a pu identifier comme étant les nombres "les plus nobles",
formant ainsi une barrière de transport interne. Les lignes magnétiques qui réussissent à
s'échapper à travers cette barrière commencent à voyager dans une vaste mer chaotique qui
s'étend jusqu'à une barrière très robuste (tant que
est le flux toroïdal caractérisant les surfaces
magnétiques (proportionnel au carré du rayon r de cette surface). Pour de faibles valeurs de L,
des surfaces magnétiques fermées existent (tores de KAM) et des chaînes d'îlots commencent
à apparaître sur les surfaces rationnelles pour des valeurs de L supérieures, avec, comme
attendu, des zones chaotiques autour des points hyperboliques. Des résidus d'îlots
magnétiques persistent dans le domaine chaotique pour toutes les valeurs de L, sur les
surfaces caractérisées par les principales valeurs rationnelles de q.
Des trajectoires individuelles de ligne magnétique indiquent la persistance d'un cœur protégé
au sein du plasma, entouré d'une couche chaotique, incluse dans une double barrière de
transport : celle-ci est composée de deux Cantori situés sur deux valeurs successives du facteur
de sécurité perturbé que l'on a pu identifier comme étant les nombres "les plus nobles",
formant ainsi une barrière de transport interne. Les lignes magnétiques qui réussissent à
s'échapper à travers cette barrière commencent à voyager dans une vaste mer chaotique qui
s'étend jusqu'à une barrière très robuste (tant que  ) qui a été identifiée mathématiquement
comme étant une surface KAM robuste au bord du plasma. Dans ce cas le mouvement
observé est intermittent, avec de longues périodes de pseudo-piégeage dans la couche
chaotique, ou du collage (sticking) autour des îlots résiduels, comme attendu pour une marche
aléatoire en temps continu.
Pour des valeurs de
) qui a été identifiée mathématiquement
comme étant une surface KAM robuste au bord du plasma. Dans ce cas le mouvement
observé est intermittent, avec de longues périodes de pseudo-piégeage dans la couche
chaotique, ou du collage (sticking) autour des îlots résiduels, comme attendu pour une marche
aléatoire en temps continu.
Pour des valeurs de  , au-dessus du seuil d'échappement, la plupart des lignes
magnétiques parviennent à s'échapper à travers la barrière externe qui est devenue un
Cantorus perméable. L'analyse statistique d'un grand nombre de trajectoires, représentant
l'évolution d'un faisceau de lignes magnétiques, indique qu'en moyenne la variable de flux ψ
croît asymptotiquement de manière diffusive (comme
, au-dessus du seuil d'échappement, la plupart des lignes
magnétiques parviennent à s'échapper à travers la barrière externe qui est devenue un
Cantorus perméable. L'analyse statistique d'un grand nombre de trajectoires, représentant
l'évolution d'un faisceau de lignes magnétiques, indique qu'en moyenne la variable de flux ψ
croît asymptotiquement de manière diffusive (comme  ) avec une loi d'échelle en L2 comme
attendu, mais avec une position radiale moyenne
) avec une loi d'échelle en L2 comme
attendu, mais avec une position radiale moyenne  ) croissant asymptotiquement comme
) croissant asymptotiquement comme
 , tandis que le déplacement quadratique moyen autour de ce rayon moyen croît
asymptotiquement de manière sous-diffusive comme
, tandis que le déplacement quadratique moyen autour de ce rayon moyen croît
asymptotiquement de manière sous-diffusive comme  . Ce résultat indique une
dispersion plus lente dans le cas étudié d'un régime de chaos incomplet, qui est différente de
la diffusion quasi-linéaire en situation de chaos complet. Pour des temps physiques
. Ce résultat indique une
dispersion plus lente dans le cas étudié d'un régime de chaos incomplet, qui est différente de
la diffusion quasi-linéaire en situation de chaos complet. Pour des temps physiques
 de
l'ordre du temps d'échappement, défini par
de
l'ordre du temps d'échappement, défini par  , le mouvement apparaît comme super-diffusif, mais cependant moins " dangereux " que la diffusion quasi-linéaire généralement
admise. On discute finalement les ordres de grandeur des temps caractéristiques dans le
tokamak TORE SUPRA.
, le mouvement apparaît comme super-diffusif, mais cependant moins " dangereux " que la diffusion quasi-linéaire généralement
admise. On discute finalement les ordres de grandeur des temps caractéristiques dans le
tokamak TORE SUPRA.
© EDP Sciences, 2003


